
Évariste Galois
➊. Nếu như những vị anh hùng kiệt xuất trong các tiểu thuyết kiếm hiệp là những nhân vật hư cấu, thì trong toán học lại có những huyền thoại mang đậm tính chân thực. Với tôi Évariste Galois (1811 – 1832) là một trong những người như thế, ông ấy cũng là người đầu tiên truyền cái đẹp của toán học đến cho tôi.
Năm học lớp 9, tình cờ có lần tôi đọc một cuốn sách toán nâng cao của cậu em họ. Khi đó toán học với tôi rất thô và nhàm chán, tôi không chú tâm đọc những bài toán cho lắm, nhưng lại thích đọc những phần Lịch Sử của nó. Lần đó ở trường tôi mới chỉ biết đến những phương trình bậc 2 với cách giải đơn giản, vì vậy mà khi thấy cuốn sách ấy đề cập đến các phương trình bậc cao hơn, tôi như một đứa trẻ vừa mới được người lớn cho kẹo. Tôi bắt đầu chú tâm đọc nó (chỉ vỏn vẹn trong 3 mặt giấy) vì nghĩ rằng nếu biết cách giải chúng thì những phương trình hay hệ phương trình ở trường kia chỉ còn là hệ quả mà thôi. Đầu tiên là những phương trình bậc 3, người công bố cách giải của những phương trình này là Gerolamo Cardano (1501 – 1576) trong cuốn Ars magna năm 1545, nhưng thực ra trước đó nó đã được đề xuất bởi Scipione del Ferro (1465 – 1526) và Niccolò Fontana Tartaglia (1499 – 1557). Cách giải của những phương trình này chỉ là những phép thế ẩn làm suy biến và đưa về giải một phương trình bậc 2 tương ứng, điều đáng chú ý là phương pháp ấy đã dẫn đến sự ra đời của số phức. Cũng theo lối giải ấy, học trò của Cardano là Lodovico Ferrari (1522 – 1565) đã tìm ra cách giải các phương trình bậc 4 bằng phép biến đổi về phương trình bậc 3 tương ứng. Sau khi đọc xong cách giải của những phương trình trên, tôi đã hiểu chúng và việc giải những phương trình ở trường của tôi trở nên vô cùng đơn giản, từ đó tôi không thấy toán học thô như mình vẫn nghĩ.
Trở lại với câu chuyện trên, khi đã đọc xong về các phương trình bậc 3 và 4, tôi bắt đầu đọc tiếp về các phương trình bậc cao hơn với hy vọng sẽ được biết thêm những điều thú vị khác, dĩ nhiên là những gì tôi mong muốn không được đáp ứng. Khi đọc đến việc Niels Henrik Abel (1802-1829) chứng minh sự không giải được của các phương trình bậc 5, sau đó là việc Évariste Galois chứng minh sự không giải được của những phương trình bậc lớn hơn 4 dưới dạng tổng quát bằng Lý thuyết nhóm của mình. Tác giả cuốn sách chỉ nói thế, phần sau cùng kể ngắn gọn về cuộc đời đầy bất hạnh của Galois. Sau khi đọc xong, tôi có phần hơi hụt hẫng, vì có những điều ngày đó tôi muốn biết mà không thể biết được. Cũng từ cái lần đó mỗi khi làm những bài toán về các phương trình ở trường, hình ảnh người hùng Évariste Galois và từ “Nhóm” (Group) lại hiện lên trong tôi.
Một dịp khác vào khoảng cuối lớp 9, khi nghỉ hè, tôi lật lại những trang sách ấy đọc 1 lần nữa, dù biết chẳng thu thập thêm được gì. Tôi đọc kỹ lại những cách giải đã biết ấy, rồi ngẫm một hồi lâu, tôi đặt những câu hỏi bên lề, đại loại như: Rõ ràng bậc 3 giải được, nhưng từ bậc 5 trở đi lại không được, vậy thì những phương trình có dạng tổng quát như thế nào thì có thể giải được ? Liệu với 1 số cho trước, có thể biết được nó là nghiệm của những phương trình với hệ số nguyên dạng nào không ?
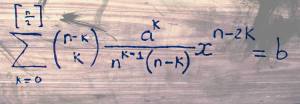
Loại phương trình đầu tiên mà tôi tìm ra
Với câu hỏi đầu tiên, và với sự “ngây thơ” ngày ấy của mình, tôi đã dành hẳn một khoảng thời gian, những tệp giấy nháp và sự hiểu biết non nớt của mình để đi đo một câu hỏi lớn như thế :). Và cũng với sự non nớt ấy, khi chưa hiểu nhóm là gì, tôi chỉ biết vận dụng trực giác cố gắng tìm những sự đối xứng tương quan trên những “khai triển mở rộng” phức tạp của mình. Cuối cùng tôi cũng tìm được một loại phương trình tổng quát “đồng tính” với những phương trình bậc 3 mà tôi đã biết, mà với phương trình tổng quát ấy, các phương trình bậc 3 chỉ còn là hệ quả nhỏ nhất. Lúc đó tôi vô cùng tâm đắc với thành quả của mình, tôi đem khoe với cậu bạn cùng lớp trong niềm sung sướng khó tả. Bây giờ nghĩ lại, thấy ngày xưa mình thật “lãng mạn”…….
➋.
Với việc tìm ra loại phương trình tổng quát trên, tôi bắt đầu bị toán học lôi cuốn, tôi cố gắng sưu tầm những cuốn sách nâng cao khác để đọc, nhưng những gì mà tôi thu được cũng chẳng khá hơn. Tôi có đọc vài cuốn sách về Lý Thuyết Số và Lượng Giác, trong đó đề cập đến số Bernoulli (1654 – 1705) và các đa thức của Pafnuty Chebyshev (1821 – 1894), các công thức này thực ra là công thức nhân dạng tổng quát của hàm sin và cos. Khi đọc xong, nhận thấy không có công thức dành cho các hàm lượng giác khác nên tôi đã tìm cách xây dựng chúng, sau này tôi mới biết rằng chúng đã tồn tại. Một vài chuyện xảy ra vào thời gian này, tôi bắt đầu tiếp xúc với những kiến thức toán mới qua internet và sao nhãng với việc học ở trường.
Kỳ thi vượt cấp đến, tôi thi vào THPT Ba Đình nhưng chỉ học ở đó năm lớp 10, đó cũng là năm bắt đầu có nhiều chuyện không tốt đối với tôi. Tôi bị trầm cảm, việc học ở trường của tôi càng ngày càng trở nên tồi tệ, bạn bè và một số giáo viên có lẽ không hài lòng về tôi. Tôi không biết phải nói gì với ai, tôi chán việc đến lớp, chán phải đối mặt với những đứa bạn, với những người mà tôi không thích. Tôi lên mạng đọc về toán để cố gắng làm vui mình, ban đầu tôi chỉ biết đọc và đọc, tôi tìm đọc về tất cả các nhà toán học mà tôi thấy người ta hay nhắc đến, dĩ nhiên là không thể thiếu người hùng Évariste Galois mà tôi cảm phục, tôi cũng sưu tầm và chép lại tất cả những định lý toán học mà tôi đọc được (khoảng gần 500 định lý, phần nhiều về hình học cổ điển).
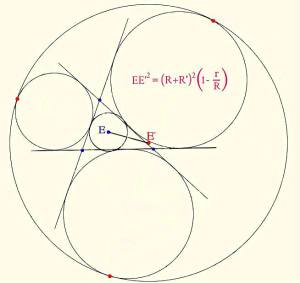
Một trong những định lý cổ điển mà tôi xây dựng
Đối với hình học cổ điển tôi khá hứng thú với các điểm, tôi đã thiết lập và đơn giản hóa một khối công thức tính khoảng cách tương đối đồ sộ giữa các điểm đặc biệt (việc đơn giản hóa chúng rất phức tạp). Tôi tìm cách tổng quát và cũng xây dựng cho mình những định lý với những cái đẹp riêng. Nhưng cái tôi tâm đắc nhất không phải là những điều kể trên, việc nắm giữ và ghi nhớ chúng đã dẫn tôi đến một hướng mới sau này trong hình học mà tôi gọi nó là Hình Học Tương Đối, nó cho phép tôi có cái nhìn phổ quát về tính chất của các đối tượng hình học, cũng như sự nhất quán giữa chúng.
Tình yêu toán học đến với tôi tình cờ và giản đơn như thế, nhưng tôi chỉ biết đặt nó trong tim mà không biết nói với ai và nói như thế nào. Cái tình yêu đó cuồng nhiệt tới mức tôi đã đem những công thức, định lý mà tôi tự khám phá ấy khoe với cô chủ nhiệm một cách rất ngây ngô…….

Georg Cantor
Những gì vĩ đại nhất luôn xuất phát từ những điều đơn giản nhất, thậm chí bị xem là ngớ ngẩn. Đó chính là then chốt trong bất kỳ một tư tưởng lớn bé nào. Với tôi, việc giác ngộ chúng cũng chỉ cần giản đơn như vậy.
Quãng thời gian năm lớp 10 cũng là lúc những cơn đau đầu dai dẳng đeo bám tôi, tôi trở nên cục tính và tiêu cực, không thích nói chuyện và bắt đầu xa lánh mọi người. Tôi lại tìm đến toán, tìm đến thú vui của riêng mình.
Quay lại với Évariste Galois, người khai sinh ra Lý thuyết nhóm, một nhánh quan trọng của Đại số trừu tượng. Nhóm thực ra là một cấu trúc với thành phần là một tập hợp kèm theo một phép toán hai ngôi trên nó thỏa mãn một hệ tiên đề nhất định. Nó đơn giản chỉ có thế, những cái khác có thể định nghĩa và triển khai dựa trên việc xem xét nó mà thôi. Tư tưởng của Galois ban đầu bắt nguồn từ vấn đề giải những phương trình đại số bậc cao, và nhóm mà ông sử dụng là nhóm hoán vị, công trình của ông được gửi nhiều lần đến Viện hàn lâm khoa học Pháp, nhưng chỉ sau khi ông mất người ta mới bắt đầu chú ý đến. Có thể nói đó là cấu trúc toán đầu tiên được hình thành trong Đại số, theo lối đó sau này những cấu trúc khác như Vành, Trường cũng được định nghĩa tương tự, đồng thời người ta cũng dùng Lý thuyết nhóm để xây dựng và phân loại hình học ( Theo Chương trình Erlangen của Felix Klein (1849 – 1925) đưa ra năm 1872).
Khi đọc về nhóm, lúc đầu tôi chưa thực sự chú tâm cho lắm vì thấy nó khá “dễ hiểu” với mình. Tôi vẫn tiếp tục hăng say với những khám phá hình học cho đến khi những ý tưởng về Biểu tính trong cái Hình học tương đối mà tôi xây dựng xuất hiện, đã dẫn tôi quay trở lại với những khái niệm Đại số, mà tiêu biểu trong số chúng là Lý thuyết tập hợp của Georg Cantor (1845 – 1918). Ông ấy chính là người thứ 2 truyền cảm hứng toán học cho tôi…….
➍. Cantor và hậu Cantor
Không ai có quyền bác bỏ tư tưởng của người khác khi họ chưa đủ thông minh và cơ sở để làm điều đó !
Năm lớp 10 trôi qua, khi ấy việc đến trường với tôi chỉ còn là hình thức. Những cơn đau đầu, những điều không tốt lặp đi lặp lại, việc không thể bày tỏ được cảm xúc của mình ra ngoài khiến tôi càng tiêu cực hơn. Có lẽ mọi người không ai chịu được khi tiếp xúc với tôi, tôi luôn cảm thấy bị cô lập tinh thần và đã không ít lần nghĩ quẩn. Cuối cùng tôi quyết định chuyển đi học tại một trường tư ở Hà Nội. Những đam mê toán học cũng tạm dừng từ đó…
Nhắc đến Cantor, có lẽ ông chỉ may mắn hơn Galois ở chỗ công trình của ông vẫn được người ta công nhận khi còn sống, nhưng không phải vì thế mà cuộc đời và sự nghiệp của ông trôi qua một cách suôn sẻ. Bên cạnh sự vinh danh dành cho ông, vẫn còn một lớp những tri thức lớn của toán học như Leopold Kronecker (1823 – 1891) (thầy của Cantor), Jules Henri Poincaré (1854 – 1912) phê phán kịch liệt Lý thuyết tập hợp, thậm chí còn công kích trực tiếp đến cá nhân Cantor, có thể vì thế đã tạo nên những cơn trầm uất mà ông phải hứng chịu trong suốt thời gian dài. Với bản thân tôi, khi đọc về Cantor và lý thuyết của ông, tôi luôn có một thắc mắc đơn giản: Tại sao lại không công nhận tập hợp, trong khi nhóm lại được định nghĩa từ khái niệm này ? Nhưng dù sao đi nữa thì những tên tuổi lớn như trên cũng không thể đem lại cho tôi một cái nhìn tốt đẹp gì cả, dẫu cho họ đã từng có những cống hiến lớn lao như thế nào cho khoa học.
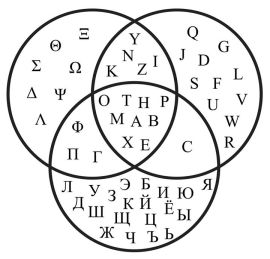
Tập hợp (minh họa theo biểu đồ Venn)
Lý thuyết về tập hợp thực ra cũng dễ hiểu, nó tạo nên từ 2 thành phần chính: Tập hợp và Lực lượng của nó, có thể hiểu đơn giản như một Nhóm, Vành, Trường hay những cấu trúc tương tự nào đó bị loại bỏ đi những phép toán, tất cả những cái còn lại được định nghĩa và triển khai từ đó. Bóng dáng của Tập hợp có thể nhìn thấy ở vô số những ngóc ngách trong toán học, nhất là trong những lý thuyết hiện đại trừu tượng và tân tiến lại càng không thể thiếu, chính vì thế mà nó được xem như nền tảng của toán học…..
➐. Tư tưởng và sự ngẫu nhiên
Trở lại với những xấp giấy cũ sau gần 4 năm bỏ dở, tôi tập trung trí tưởng tượng của mình vào cái giả thuyết mông lung hồi lớp 10 nhiều hơn: Mọi chân lý đều như nhau. Đó là một ý tưởng rất “điên rồ” và táo bạo, những gì mà tôi biết không thể giúp tôi trả lời được, vì vậy đòi hỏi tôi phải tự tìm cách xây dựng nên những cơ sở riêng để tiếp cận nó. Tôi đã phác thảo một sơ đồ trong đầu và quyết định tiếp cận nó theo chiều phạm vi từ nhỏ đến lớn :
![]()
Đối với hình học, việc ghi nhớ những đặc điểm chung ẩn bên trong các đối tượng, cùng với cách thức mà chúng khác biệt nhau đã dẫn tôi đến những khái niệm đầu tiên của Hình học tương đối, trong đó có 2 thành phần chủ chốt là Hình và các Phép kiến hình. Sau một khoảng thời gian cố gắng tổng hợp và biểu diễn chúng lên những trang giấy, cuối cùng cái hệ thống tương đối cho hình học cổ điển mà tôi mong muốn cũng dần dần xuất hiện, đó là bước then chốt mở đầu cho những phát kiến của tôi sau đó. Tuy nhiên trong quá trình xây dựng chúng, tôi gặp phải một khó khăn đối với Hình học phi Euclid và những liên hệ với Hình học Fractal của Benoit Mandelbrot (1924 – 2010). Một cách tự nhiên khái niệmBiểu tính đến với tôi, nó như một chiếc chìa khóa diệu kỳ đưa trí tưởng tượng của tôi đi sâu và xa hơn, một lần nữa tôi quay lại với Lý thuyết tập hợp và hướng sự chú ý đặc biệt tới những lý thuyết mới kinh điển như: Lý thuyết phạm trù, Hình học đại số và một nhân vật tầm cỡ của thế kỷ 20, đó là Alexander Grothendieck (1928).
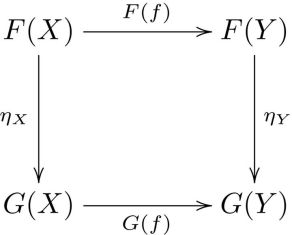
Phạm Trù
Lý thuyết phạm trù được đưa ra lần đầu tiên bởi Saunders Mac Lane (1909 – 2005) và Samuel Eilenberg (1913 – 1998), thành phần chính của nó gồm: Phạm trù, Hàm tử và Cấu xạ giữa các hàm tử (Các phép biến đổi tự nhiên). Dưới cái nhìn của tôi, Lý thuyết phạm trù về cơ bản cũng không khác Lý thuyết tập hợp của Cantor cho lắm, nhưng nó cho ta một cái nhìn tổng quan và có thể xem như là một ngôn ngữ tổng quát của Đại số (từ nó ta dễ dàng nhìn thấy các khái niệm khác như: Nhóm, Vành, Trường, các không gian topo, metric, v.v, và dĩ nhiên là cả cácTập hợp).

Hình Học Đại Số
Hình học đại số thì có thể hiểu đơn giản như cái tên của nó, đó là môn hình học được xây dựng và mô tả bằng ngôn ngữ của đại số, nó chớm nở từ thời Hi Lạp cổ đại nhưng chỉ bắt đầu phát triển rầm rộ ở Italia vào khoảng cuối thế kỷ 19. Nó là sản phẩm của các thế hệ nhà toán học và công cụ chủ chốt của nó là Đại số giao hoán và Phạm trù.

Alexander Grothendieck
